How Do We Simplify Radicals?

Step 1: Find all the " Prime Factors" starting with the smallest Prime 
Step 2: Rewrite using square Notations
Step 3: Separate square root notations 


Example: Simplify .

180 = 2·  90 = 2· 2· 45 = 2· 2· 9· 5 = 2· 2· 3· 3· 5

Therefore,

 = 2· 3 = 6.

here is a video to help you understand better

How do we Factor the difference of squares?

This expression is called a difference of two squares. 

The factors of          are and     

Example 1:

Factor:   x2 - 9Both x2 and 9 are perfect squares.  Since subtraction is occurring between these squares, this expression is the difference of two squares. What times itself will give x2 ?  The answer is x. What times itself will give 9 ?  The answer is 3. These answers could also be negative values, but positive values will make our work easier. The factors are (x + 3) and (x - 3). Answer:  (x + 3) (x - 3)  or   (x - 3) (x + 3)   (order is not important)

Here is a video to help you understand better....

How do we divide polynomials?

 Simplify 

Factor out the common factor from the top and bottom, and then cancel off:

X = 2




Here is a video to help explain how to divide polynomials:

How do we identify all the Elements of a Parabola?

When you have the formula to graph a Parabola you need to be able to understand what it stands for/ says....


                      y = ax² + bx + c
The  A for how wide or how narrow the parabola will be.
The   B stands for the line of symmetry
The  C tells you if its will be facing up or will be facing down.( If a Parabola is facing down the C is negative but if its facing up then the C is Positive)




To find the axis of symmetry you use the formula......






          X  = -  B
                       
                  2A


Roots are where and when the parabola touches the X-axis 

How do we Graph Parabolas?

Graphing the Parabola y = ax2 + bx + c


1.    Determine whether the parabola opens upward or downward.


                 a.    If a is positive, it opens upward.
                b.    If a negative, it opens downward.


2.    Determine the vertex.
             a.    The x-coordinate is .
                 b.    The y-coordinate is found by substituting the x-coordinate, from Step 2a, in the equation                                                     y = ax^2 + bx + c.


3.    Determine the y-intercept by setting x = 0.

by determining all the key features of the graph. That is, find the vertex, the x- and y-intercepts (if any), and additional points if needed. Find the domain and range of the function.

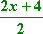
Opens upward since the coefficient of the x² is positive  

4.    Determine the x-intercepts (if any) by setting y = 0, i.e., solving the equation 
       ax2 + bx + c = 0.


5.    Determine two or three other points if there are no x-intercepts.



For Example:

Graph  

Vertex:  and  So the vertex is (3, -4).

y-intercept:  The y-intercept is (0,5).

x-intercepts:

                            

The x-intercepts are (5,0) and (1,0).

        Points plotted on grid below:

 Then connect the points with a smooth curve.
Here is A video to help you understand better how to graph a Parabola.

How do we solve rational Proportions?

Solve...
                   k+4             K+9
                --------  =    --------
                     2                 3
Step 1 : multiply each side by a number to get a common denominator

          3  *  k+4             K+9  *3

                --------  =    --------

          3*      2                 3      *3

Step 2:  you cancel the  denominator  because their the same 

          

                 3k+12          2K+18

                --------  =    --------

                     6                6

Step 3: start to subtract, add , divide, or multiply to both sides to cancel out terms to get x by its self and to equal to a number

          3k + 12 = 2k +18

        -2k           -2k

                                         

          k + 12 = 18

             -12     -12

                                         

                 k = 6

How do we solve rational Expression?

Simplify the following Expression.....

                                                2                  3

                                            ------     -     -------

                                               A                  A^2

Step 1: Change fractions into equivalent fractions with a common denominator

                                      A *    2                  3

                                            ------     -     -------

                                   A*      A                  A^2

Step 2: add or subtract  numerators, keep the common denominator

                                                2                  3                    2A -  3

                                            ------     -     -------       =   ------------

                                              A^2                 A^2                A^2

Step 3:Simplify the resulting expression, cancelling common factor

                               2A -  3

                           ------------     ( because the expression does not  simplify any more this is your final answer)

                                 A^2