y = x^2 - 2x + 2
y - 2x = - 2 Step 1: First you have to change this into standard form : Y = MX +B )
+2x +2x
----------------
Y = 2x - 2
2x - 2 = x^2 - 2x +2 Step 2) Substitute this variable into the quadratic equation
-2x +2 -2x+2
---------------------
0 = X^2 -4x +4 Step 3) Solve the quadratic equation
0=(x - 2)(x - 2)
You have to make the equation equal Zero so if it`s positive to make it zero you have to make it negative, so if it`s negative you have to make it Positive.
For example :
0 = (x - 2)
X has to be positive 2
But if it was 0 = (x +2)
X would have to be negative 2
So the value of X is 2 so what you do next is Step 4) Substitute x value into linear equation to get y value
y = 2x- 2 = 2(2)- 2 = 2
Solution = (2,2)
Wednesday, May 2, 2012
Monday, April 16, 2012
How Do We use the discriminant to Find the Number of Solutions To a Quadratic Equation?
The solutions to a quadratic Equation is when the Parabola touches the X- axis which are also called the "roots".
The Discriminant is B^2 - 4AC
If B^2 - 4ac > 0 you`ll get two solutions
If B^2 - 4ac = 0 you`ll get one solution
If B^2 - 4ac < 0 you`ll get no solution
For example :
X^2 + 6X + 9 = 0
A = 1 B^2 - 4ac = ?
B = 6 6^2 - 4(1)(9)
C = 9 36 - 36 = 0
(One solution) because its equal to Zero
Another example:
-16x^2 + 11x - 11 = 0
A = -16 B^2 - 4ac =?
B = 11 11^2 - 4(-16)(-11)
C = -11 121-+ 64(-11)
121 + -704
-583
(NO solution) because its less then Zero
Example:
5x^2 + 2x - 10 = 0
A=5 b^2 - 4ac
B=2 2^2 - 4(5)(-10)
C=-10 4- 200
204
( Two solutions) because its greater then Zero
The Discriminant is B^2 - 4AC
If B^2 - 4ac > 0 you`ll get two solutions
If B^2 - 4ac = 0 you`ll get one solution
If B^2 - 4ac < 0 you`ll get no solution
For example :
X^2 + 6X + 9 = 0
A = 1 B^2 - 4ac = ?
B = 6 6^2 - 4(1)(9)
C = 9 36 - 36 = 0
(One solution) because its equal to Zero
Another example:
-16x^2 + 11x - 11 = 0
A = -16 B^2 - 4ac =?
B = 11 11^2 - 4(-16)(-11)
C = -11 121-+ 64(-11)
121 + -704
-583
(NO solution) because its less then Zero
Example:
5x^2 + 2x - 10 = 0
A=5 b^2 - 4ac
B=2 2^2 - 4(5)(-10)
C=-10 4- 200
204
( Two solutions) because its greater then Zero
How Do We Work with quadratics?
The first thing that you should think of when you think of quadratics is the
Quadratic Equation:

So if you have the equation x^2 + 2x - 1
A = 1
B = 2
The value of C is the number without an x after it
C = -1
Step 1: plug in
Step 2 : simplify
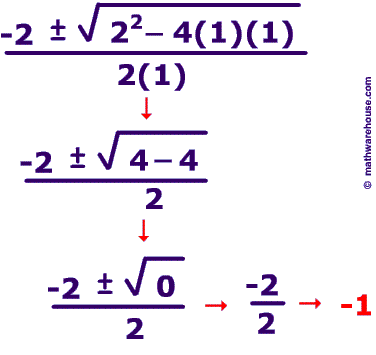
Quadratic Equation:

So if you have the equation x^2 + 2x - 1
- First you have to find the value of A, B and C
- The value of A is in front of the first x
A = 1
- The value of B is in front of the second X
B = 2
The value of C is the number without an x after it
C = -1
Step 1: plug in
Step 2 : simplify
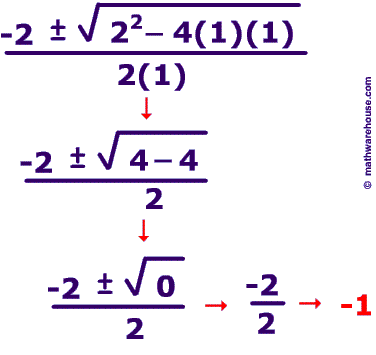
Sunday, March 18, 2012
How Do We Simplify Radicals?
Step 1: Find all the " Prime Factors" starting with the smallest Prime
Step 2: Rewrite using square Notations
Step 3: Separate square root notations
Example: Simplify .
.
 = 2· 3
= 2· 3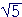 = 6
= 6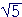 .
.
Step 2: Rewrite using square Notations
Step 3: Separate square root notations
Example: Simplify
180 = 2· 90 = 2· 2· 45 = 2· 2· 9· 5 = 2· 2· 3· 3· 5
Therefore,
here is a video to help you understand better
Thursday, March 15, 2012
How do we Factor the difference of squares?
This expression is called a difference of two squares.
The factors of  are
are  and
and 
Here is a video to help you understand better....
 are
are  and
and 
Example 1:
Factor: x2 - 9Both x2 and 9 are perfect squares. Since subtraction is occurring between these squares, this expression is the difference of two squares.
Answer: (x + 3) (x - 3) or (x - 3) (x + 3) (order is not important) |
How do we divide polynomials?
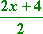
Factor out the common factor from the top and bottom, and then cancel off:
X = 2
Here is a video to help explain how to divide polynomials:
Monday, March 12, 2012
How do we identify all the Elements of a Parabola?
When you have the formula to graph a Parabola you need to be able to understand what it stands for/ says....
y = ax2 + bx + c
The A for how wide or how narrow the parabola will be.
The B stands for the line of symmetry
The C tells you if its will be facing up or will be facing down.( If a Parabola is facing down the C is negative but if its facing up then the C is Positive)
To find the axis of symmetry you use the formula......
X = - B
2A
Roots are where and when the parabola touches the X-axis
y = ax2 + bx + c
The A for how wide or how narrow the parabola will be.
The B stands for the line of symmetry
The C tells you if its will be facing up or will be facing down.( If a Parabola is facing down the C is negative but if its facing up then the C is Positive)
To find the axis of symmetry you use the formula......
X = - B
2A
Roots are where and when the parabola touches the X-axis
How do we Graph Parabolas?
Graphing the Parabola y = ax2 + bx + c
1. Determine whether the parabola opens upward or downward.
a. If a is positive, it opens upward.
b. If a negative, it opens downward.
2. Determine the vertex.
a. The x-coordinate is .

b. The y-coordinate is found by substituting the x-coordinate, from Step 2a, in the equation y = ax^2 + bx + c.
3. Determine the y-intercept by setting x = 0.
by determining all the key features of the graph. That is, find the vertex, the x- and y-intercepts (if any), and additional points if needed. Find the domain and range of the function.
Opens upward since the coefficient of the x2 is positive
4. Determine the x-intercepts (if any) by setting y = 0, i.e., solving the equation
ax2 + bx + c = 0.
5. Determine two or three other points if there are no x-intercepts.
For Example:
Graph 
Vertex:and
So the vertex is (3, -4).
y-intercept:The y-intercept is (0,5).
x-intercepts:

The x-intercepts are (5,0) and (1,0).
Points plotted on grid below:
Then connect the points with a smooth curve.
 Here is A video to help you understand better how to graph a Parabola.
Here is A video to help you understand better how to graph a Parabola.Sunday, March 4, 2012
How do we solve rational Proportions?
Solve...
k+4 K+9
-------- = --------
2 3
Step 1 : multiply each side by a number to get a common denominator
6 6
-12 -12
k+4 K+9
-------- = --------
2 3
Step 1 : multiply each side by a number to get a common denominator
3 * k+4 K+9 *3
-------- = --------
3* 2 3 *3
Step 2: you cancel the denominator because their the same
3k+12 2K+18
-------- = --------
Step 3: start to subtract, add , divide, or multiply to both sides to cancel out terms to get x by its self and to equal to a number
3k + 12 = 2k +18
-2k -2k
k + 12 = 18
k = 6
How do we solve rational Expression?
Simplify the following Expression.....
2 3
------ - -------
A A^2
Step 1: Change fractions into equivalent fractions with a common denominator
A * 2 3
------ - -------
A* A A^2
Step 2: add or subtract numerators, keep the common denominator
2 3 2A - 3
------ - ------- = ------------
A^2 A^2 A^2
Step 3:Simplify the resulting expression, cancelling common factor
2A - 3
------------ ( because the expression does not simplify any more this is your final answer)
A^2
Friday, February 10, 2012
How do we solve diamond problems?
First you will have a shape that look like a diamond (like the picture below). You will notice that 2 of the spaces are filled in. You have to use the pattern to be able to fill the other two out. The pattern is to have the two other numbers to add to the number on top and to be able to multiply to the number on the bottom. You do this by using the factors of the number you are going to multiply.
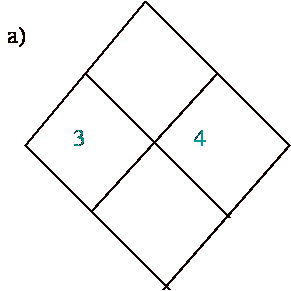
For example you will multiply 3 and 4 which gives you 12 which would go on the bottom. Then you add 3 and 4 which would be 7.
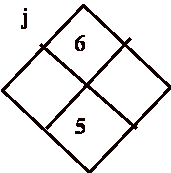 For example you have to figure out what can be multiply to get 5 and then what can also be added to 6. So first you use the factors of 5 which are 5 and 1 , so when you multiply 5 and 1 you get 5, and when you add 5 and 1 you get 6. So the only two numbers you can use to to fill the diamond out correctly if 5 and 1.
For example you have to figure out what can be multiply to get 5 and then what can also be added to 6. So first you use the factors of 5 which are 5 and 1 , so when you multiply 5 and 1 you get 5, and when you add 5 and 1 you get 6. So the only two numbers you can use to to fill the diamond out correctly if 5 and 1.

For example you will multiply 3 and 4 which gives you 12 which would go on the bottom. Then you add 3 and 4 which would be 7.
 For example you have to figure out what can be multiply to get 5 and then what can also be added to 6. So first you use the factors of 5 which are 5 and 1 , so when you multiply 5 and 1 you get 5, and when you add 5 and 1 you get 6. So the only two numbers you can use to to fill the diamond out correctly if 5 and 1.
For example you have to figure out what can be multiply to get 5 and then what can also be added to 6. So first you use the factors of 5 which are 5 and 1 , so when you multiply 5 and 1 you get 5, and when you add 5 and 1 you get 6. So the only two numbers you can use to to fill the diamond out correctly if 5 and 1.Monday, February 6, 2012
Classify Polynomials
How do we classify polynomials?
First you find the degree of the polynomials for example: Fourth degree , cubic, linear quadratic, and constant. Then you have to figure out what kind of polynomial it is like a monomial , binomials ,or trinomial. You have to remember to put it in standard form which just means to put the polynomials in order from greatest to least by the exponents.
First you find the degree of the polynomials for example: Fourth degree , cubic, linear quadratic, and constant. Then you have to figure out what kind of polynomial it is like a monomial , binomials ,or trinomial. You have to remember to put it in standard form which just means to put the polynomials in order from greatest to least by the exponents.
Subscribe to:
Comments (Atom)


