y = x^2 - 2x + 2
y - 2x = - 2 Step 1: First you have to change this into standard form : Y = MX +B )
+2x +2x
----------------
Y = 2x - 2
2x - 2 = x^2 - 2x +2 Step 2) Substitute this variable into the quadratic equation
-2x +2 -2x+2
---------------------
0 = X^2 -4x +4 Step 3) Solve the quadratic equation
0=(x - 2)(x - 2)
You have to make the equation equal Zero so if it`s positive to make it zero you have to make it negative, so if it`s negative you have to make it Positive.
For example :
0 = (x - 2)
X has to be positive 2
But if it was 0 = (x +2)
X would have to be negative 2
So the value of X is 2 so what you do next is Step 4) Substitute x value into linear equation to get y value
y = 2x- 2 = 2(2)- 2 = 2
Solution = (2,2)
Alegbra
Wednesday, May 2, 2012
Monday, April 16, 2012
How Do We use the discriminant to Find the Number of Solutions To a Quadratic Equation?
The solutions to a quadratic Equation is when the Parabola touches the X- axis which are also called the "roots".
The Discriminant is B^2 - 4AC
If B^2 - 4ac > 0 you`ll get two solutions
If B^2 - 4ac = 0 you`ll get one solution
If B^2 - 4ac < 0 you`ll get no solution
For example :
X^2 + 6X + 9 = 0
A = 1 B^2 - 4ac = ?
B = 6 6^2 - 4(1)(9)
C = 9 36 - 36 = 0
(One solution) because its equal to Zero
Another example:
-16x^2 + 11x - 11 = 0
A = -16 B^2 - 4ac =?
B = 11 11^2 - 4(-16)(-11)
C = -11 121-+ 64(-11)
121 + -704
-583
(NO solution) because its less then Zero
Example:
5x^2 + 2x - 10 = 0
A=5 b^2 - 4ac
B=2 2^2 - 4(5)(-10)
C=-10 4- 200
204
( Two solutions) because its greater then Zero
The Discriminant is B^2 - 4AC
If B^2 - 4ac > 0 you`ll get two solutions
If B^2 - 4ac = 0 you`ll get one solution
If B^2 - 4ac < 0 you`ll get no solution
For example :
X^2 + 6X + 9 = 0
A = 1 B^2 - 4ac = ?
B = 6 6^2 - 4(1)(9)
C = 9 36 - 36 = 0
(One solution) because its equal to Zero
Another example:
-16x^2 + 11x - 11 = 0
A = -16 B^2 - 4ac =?
B = 11 11^2 - 4(-16)(-11)
C = -11 121-+ 64(-11)
121 + -704
-583
(NO solution) because its less then Zero
Example:
5x^2 + 2x - 10 = 0
A=5 b^2 - 4ac
B=2 2^2 - 4(5)(-10)
C=-10 4- 200
204
( Two solutions) because its greater then Zero
How Do We Work with quadratics?
The first thing that you should think of when you think of quadratics is the
Quadratic Equation:

So if you have the equation x^2 + 2x - 1
A = 1
B = 2
The value of C is the number without an x after it
C = -1
Step 1: plug in
Step 2 : simplify
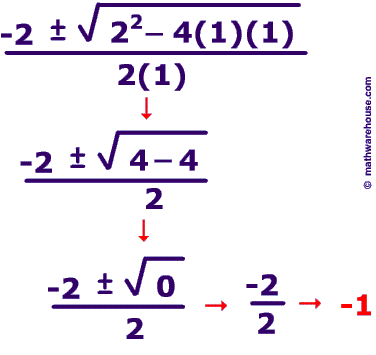
Quadratic Equation:

So if you have the equation x^2 + 2x - 1
- First you have to find the value of A, B and C
- The value of A is in front of the first x
A = 1
- The value of B is in front of the second X
B = 2
The value of C is the number without an x after it
C = -1
Step 1: plug in
Step 2 : simplify
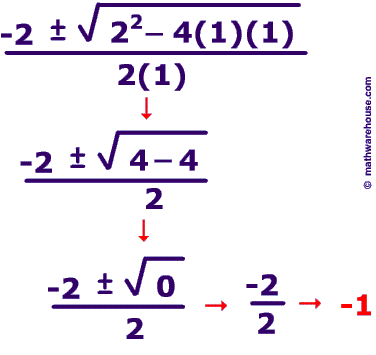
Sunday, March 18, 2012
How Do We Simplify Radicals?
Step 1: Find all the " Prime Factors" starting with the smallest Prime
Step 2: Rewrite using square Notations
Step 3: Separate square root notations
Example: Simplify .
.
 = 2· 3
= 2· 3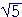 = 6
= 6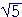 .
.
Step 2: Rewrite using square Notations
Step 3: Separate square root notations
Example: Simplify
180 = 2· 90 = 2· 2· 45 = 2· 2· 9· 5 = 2· 2· 3· 3· 5
Therefore,
here is a video to help you understand better
Thursday, March 15, 2012
How do we Factor the difference of squares?
This expression is called a difference of two squares.
The factors of  are
are  and
and 
Here is a video to help you understand better....
 are
are  and
and 
Example 1:
Factor: x2 - 9Both x2 and 9 are perfect squares. Since subtraction is occurring between these squares, this expression is the difference of two squares.
Answer: (x + 3) (x - 3) or (x - 3) (x + 3) (order is not important) |
How do we divide polynomials?
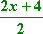
Factor out the common factor from the top and bottom, and then cancel off:
X = 2
Here is a video to help explain how to divide polynomials:
Monday, March 12, 2012
How do we identify all the Elements of a Parabola?
When you have the formula to graph a Parabola you need to be able to understand what it stands for/ says....
y = ax2 + bx + c
The A for how wide or how narrow the parabola will be.
The B stands for the line of symmetry
The C tells you if its will be facing up or will be facing down.( If a Parabola is facing down the C is negative but if its facing up then the C is Positive)
To find the axis of symmetry you use the formula......
X = - B
2A
Roots are where and when the parabola touches the X-axis
y = ax2 + bx + c
The A for how wide or how narrow the parabola will be.
The B stands for the line of symmetry
The C tells you if its will be facing up or will be facing down.( If a Parabola is facing down the C is negative but if its facing up then the C is Positive)
To find the axis of symmetry you use the formula......
X = - B
2A
Roots are where and when the parabola touches the X-axis
Subscribe to:
Comments (Atom)

